Pédagogie

               Il est de la plus grande importance de faire travailler très à fond, et dans les classes élémentaires, cette partie si importante de l’enseignement des mathématiques, appelée calcul oral.

              Les élèves devront donc calculer chaque jour oralement et surtout ne jamais compter sur leurs doigts, habitude déplorable dont on n’arrive pas à se défaire facilement. Il faut les accoutumer de bonne heure à la combinaison des nombres et pour leur en faciliter la composition et la décomposition, ils devront se servir du boulier de la façon suivante :

              1° Commencer par la 1ère rangée en comptant 1 sur la première boule de couleur et en terminant 10 sur la boule noire (toutes les boules noires, d’ailleurs, marquent les dizaines).

              2° Quand on se sert du boulier pour l’addition, on doit mettre le nombre de boules indiquées par chaque colonne à la suite les unes des autres, et non pas les prendre sur des rangées différentes.

                   Par exemple, si l’on a à additionner 8 + 5 + 4 + 7, on commence par pousser 8 boules de la 1ère rangée puis pour faire 5 les deux qui terminent cette rangée avec les 3 premières de la rangée suivante, ce qui donne 13 : on en pousse 4 à côté des 3 de la 2e rangée, et l’on a 17 ; enfin, pour ajouter encore 7, il reste à pousser les 3 qui terminent la 2e rangée et les 4 premières du commencement de la 3e rangée. On voit de suite que l’on obtient 24.

              Cette façon de procéder a le grand avantage de faire composer et décomposer les nombres à des enfants encore assez jeunes et sans les fatiguer. De plus, elle les exerce très rapidement au calcul mental car, au bout de six mois, la plupart peuvent compter de tête, sans boulier, sans se servir de leurs doigts, et sans être exposés à commettre les erreurs si fréquentes que l’on rencontre dans presque toutes les opérations des élèves.

              3° Quand on veut se servir du boulier pour la soustraction, on met sur la 1ère rangée le nombre de boules indiquées par le chiffre du nombre inférieur et on ajoute autant de boules qu’il est nécessaire pour arriver au nombre supérieur. Autrement dit on fait la soustraction par l’addition, ce qui est une autre façon de combiner les nombres.

              Exemple : mettons qu’il faille ôter 8 de 13. On commence par pousser les 8 premières boules de la première rangée : puis il s’agit d’ajouter autant de boules qu’il en faut pour arriver à 13. On poussera donc les deux boules qui terminent cette première rangée et les 3 qui commencent la deuxième rangée. On s’aperçoit alors qu’on a dû ajouter 5 boules, et il reste bien 5, car, si on enlève maintenant les 8 premières boules, il n’y a plus que les 5 boules que l’on a été obligé d’ajouter pour faire 13.

              4e On ne se sert jamais du boulier pour la multiplication et la division.

(De l'emploi du boulier par Rosalie HATTEMER - Paris, 1925)

Les outils pédagogiques

5. Les bouliers compteurs et numérateurs

Le boulier est un appareil composé d’un cadre rectangulaire muni de tiges sur lesquelles coulissent des boules servant à calculer.

Les différents bouliers

par A. Lenient,  Journal des instituteurs, 25 février 1877.

Le boulier primitif, le boulier-compteur proprement dit, celui qui se compose de tringles horizontales portant chacune neuf boules, ne peut guère servir qu’à compter, à donner aux enfants la notion du nombre, et à leur faire comprendre le principe et le but des quatre opérations fondamentales de l’arithmétique.

Même dans cette mesure il peut être, pour une institutrice et un instituteur intelligents et zélés, l’occasion et le moyen d’une foule d’exercices intéressants. Nos directrices de salles d’asile en tirent un excellent parti ; il serait fort à désirer que toutes nos classes du cours élémentaire de garçons et de filles en fussent également pourvues.

La numération écrite devant être, menée de front avec la numération parlée, il était naturel qu’on cherchât à faire servir aussi le boulier à l’étude de la représentation des nombres.

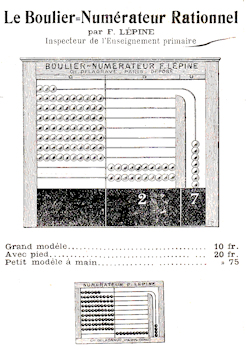
Le boulier-numérateur de Marie Pape Carpantier

Mme Pape-Carpantier, s’inspirant de modèles déjà connus, fit exécuter un boulier-numérateur qui a gardé son nom.

C’est un cadre traversé par onze tiges de fer, dont les deux plus élevées sont complètement horizontales, et les neuf autres, d’abord horizontales du côté droit, sont courbées de manière à venir se fixer verticalement sur une traverse inférieure.

« Quinze boules d’égale grosseur sont enfilées sur chacune des deux tiges supérieures, et neuf autres boules sur chacune des neuf autres tiges. Les grosseurs de ces dernières sont graduées d’une tige à l’autre, et disposées de telle sorte que lorsque les boules sont amenées dans la partie verticale de leurs tiges respectives, elles représentent des unités d’autant plus fortes qu’on avance vers la gauche. Comme il n’y a que neuf boules dans chaque tige, l’enfant est frappé de l’impossibilité de former le nombre dix, autrement qu’en avançant d’une colonne à gauche, c’est-à-dire en passant à l’unité de l’ordre supérieur. »

Cet appareil, tout en se prêtant aux divers exercices du boulier-compteur, initie de plus les enfants aux principes et aux règles de la numération écrite. La différence de grosseur des houles, et surtout la place qu’elles occupent sur les parties verticales des tiges indiquent assez clairement la valeur relative des unités qu’elles représentent. Puis, des cartons mobiles, portant chacun un des dix chiffres, permettent au maître de faire poser, au-dessous de chaque tige, le chiffre correspondant au nombre de boules que porte cette tige. L’enfant, de cette façon, aperçoit facilement le rapport qu’il y a entre le chiffre et le nombre que ce chiffre représente ; il est même ainsi conduit facilement à représenter des nombres de deux et de plusieurs chiffres.

Mais ces cartons mobiles, malheureusement, peuvent s’égarer; puis, l’enfant est bien exercé â lire les nombres, à les composer, à les décomposer et à les représenter, mais il ne les écrit pas lui-même. Il ne trace pas les chiffres; il les trouve tout faits et les pose seulement.

Le désir de remédier à cet inconvénient, ou plutôt de combler cette lacune, a fait inventer, depuis le boulier de Mme Pape, un grand nombre de numérateurs. Les meilleurs, à notre avis, sont ceux de M. Antoine et de M. Bardot, encore inédits, si je ne me trompe.

Le numérateur de M. Antoine (maître de pension à Oran), se compose d’une boîte de forme rectangulaire, dans laquelle sont placées, à côté l’une de l’autre, des tringles en bois glissant dans des coulisses fixées sur le fond de la boite. Ces tringles, que l’on fait mouvoir au moyen de boulons de cuivre qui passent dans des rainures pratiquées à la partie inférieure du dessus du numérateur, portent chacune les dix chiffres, à l’exception de la première de droite qui porte des points ronds représentant la valeur de ces dix chiffres. Les chiffres et les points ronds apparaissent dans le mouvement de bas en haut ou de haut en bas des tringles, à une ouverture transversale ménagée dans la partie moyenne de la boîte. Chaque tringle ne peut ainsi présenter qu’un chiffre à la fois.

Il y a dix tringles, y compris celle des points. Le nombre des tringles à chiffres est de neuf ; mais il pourrait être plus considérable.

Les initiales des mots unités, dizaines et centaines, qui désignent chaque ordre, placées sur une petite plaque au-dessus de chaque tringle, indiquent les unités simples, les dizaines et les centaines de chaque classe, et ces classes, présentant chacune une couleur spéciale, sont indiquées par les mots unités, mille, millions, etc.

Un tableau noir mobile, adapté au bas du numérateur, permet à l’élève d’ajouter la pratique à la théorie, d’écrire les nombres qu’il a représentés à l’aide des tringles du numérateur.

Voici comment on se sert de cet appareil :

La tringle des points ronds, la première de droite, indique, en marchant de pair avec celle des unités simples, que les nombres s’obtiennent par l’addition de l’unité à elle-même ou au nombre déjà obtenu. Les chiffres de la tringle des unités simples correspondant aux points ronds indiquent la manière de représenter la valeur de ces points. C’est en cela que le numérateur complète le boulier-compteur.

Lorsque l’élève connaît parfaitement les dix chiffres, la tringle des points devenant inutile, ce sera le moment de faire voir à l’enfant qu’un seul de ces dix chiffres ne suffit pas pour former le nombre dix, le zéro n’ayant aucune valeur par lui-même. On fera donc apparaître, au moyen de la troisième tringle, la première dizaine, dont il sera facile de trouver la place par l’initiale D placée en regard des unités de cet ordre. On fera remarquer que cette dizaine restant fixe, il faudra faire passer successivement à côté d’elle les neufs premiers chiffres, ce qui donnera ainsi 11, 12, 13... et 19. Alors 10 se représentant de nouveau, il faudra faire voir aux élèves que la dizaine seule change en s’augmentant de 1 comme pour les unités simples.

On opérera pour la deuxième dizaine comme pour la première; de même pour les centaines et ainsi de suite.

M. Antoine a complété son numérateur de façon à ce qu’il puisse servir pour l’enseignement de la numération décimale et celle des diverses sous-unités du système métrique.

Dans ce but, il a ajouté à son instrument une petite plaque qui porte les initiales d, c, m, des mots dixièmes, centièmes, millièmes.

Les initiales d, c, m, M, D, H, H, écrites à la partie supérieure de la petite plaque, signifient respectivement dixièmes, centièmes, millièmes, mètres, décamètres, etc.

Il sera donc facile de faire comprendre, par la position même de la plaque, la relation qui existe entre la partie entière ou fractionnaire d’un nombre décimal et les différents ordres d’unités du système métrique.

Ces plaques, qui sont mobiles et qui peuvent être en nombre égal aux diverses unités du système métrique, se placent au-dessus de la petite ouverture transversale du numérateur.

Chaque exercice sur les chiffres, on le comprend, doit nécessairement être reproduit par l’élève sur le tableau noir adapté au bas du numérateur.

Sans contester son mérite et sa supériorité sur les appareils qui l’ont précédé, nous sommes obligé de constater que ce numérateur ne se prête point facilement à tous les exercices de calcul, à toutes les opérations de composition et de décomposition que permet d’effectuer l’ancien boulier-compteur.

Une seule tringle porte les neuf premiers nombres représentés par des séries de points ; comment donc le maître pourra-t-il faire comprendre à l’élève la composition d’un nombre renfermant des centaines, des dizaines et des unités? Ce numérateur, excellent pour la numération écrite, me paraît donc insuffisant au point de vue de la numération parlée, de l’étude de la formation des nombres. Je sais bien que c’est là le défaut généralement commun à tous les bouliers-numérateurs; aussi les inventeurs préparent-ils, presque tous, à l’usage de leur instrument par des exercices de calcul sur des jetons, des boules, ou des objets quelconques.

En outre, dans le numérateur-Antoine, la partie importante de l’instrument, la fenêtre horizontale à laquelle apparaissent les chiffres et les nombres, n’occupe qu’une portion très minime de la boîte. L’œil, au premier abord, ne l’aperçoit pas : il est attiré au contraire par les boutons de cuivre très apparents qui servent à faire mouvoir les tringles et par les longues fenêtres verticales dans lesquelles glissent ces tringles, dont les autres chiffres apparaissent en partie et viennent ainsi distraire l’attention de l’élève.

Ce ne sont là, fort heureusement, que des défauts d’exécution, qui pourront sans doute facilement disparaître lorsque l’auteur, l’honorable M. Antoine, livrera son invention à la publicité.

Le numérateur-Bardot me semble supérieur à la plupart de ceux qui sont actuellement en usage.

Comme tous, il substitue à l’enseignement abstrait l’enseignement direct ou par l’aspect, mais il offre sur les autres l’avantage de présenter un système complet, d’un maniement très simple, permet tant de résoudre, d’une façon apparente et sensible, toutes les questions relatives à la numération, à l’addition et à la soustraction.

Dix prismes décagonaux, rangés à côté les uns des autres, portent, sur chacune de leurs dix faces, à la partie inférieure, les séries de points de 1 à 10, et, à la partie supérieure, le chiffre correspondant à ce même nombre de points.

Mobiles sur leurs axes respectifs, ces dix prismes peuvent, par une disposition commode et simple, présenter à volonté, à la fenêtre ménagée dans le tableau, l’une quelconque de leurs faces.

Des couleurs différentes et un léger écartement groupent les prismes trois par trois, pour distinguer entre elles les unités principales, et des points de formes différentes sont affectés aux unités, aux dizaines et aux centaines de chaque groupe.

Un nombre quelconque de 1 à dix chiffres peut donc, on levait, être facilement représenté, composé et analysé par l’enfant.

En outre, ce numérateur, comme celui de M. Antoine, dans sa partie inférieure, est un véritable tableau noir, sur lequel les élèves peuvent écrire les nombres dont ils viennent d’étudier la composition et la formation, et dont ils voient, sous leurs yeux, la représentation figurée et chiffrée tout à la fois.

Les nombres, dans le Numérateur-Bardot, se présentent ainsi aux yeux de l’enfant, décomposés en groupes naturels, comprenant chacun les trois ordres d’unités disposés comme l’exigent leurs valeurs relatives; et les signes conventionnels ou chiffres apparaissent en même temps que les groupes naturels qu’ils représentent. De cette façon, le signe reste donc inséparable de la chose signifiée : condition des plus favorables pour graver la forme et la valeur du chiffre ou du nombre dans l’esprit de l’enfant.

La numération parlée et la numération écrite peuvent, avec le Numérateur-Bardot, être étudiées, à volonté, séparément comme l’indiquent la plupart des programmes des écoles pour le cours élémentaire, on simultanément, si on le désire, et comme il est bon de le faire, nous l’avons dit.

De plus, une courroie sans fin transporte, où l’on veut, une virgule mobile destinée à séparer les unités entières des unités décimales, de telle sorte que l’appareil permet de représenter les nombres décimaux avec autant de facilité que les nombres entiers, et de faire effectuer aux élèves, en les leur expliquant, les multiplications par 10, 100, 1000, etc.

Quant au mécanisme de l’addition et de la soustraction, il est rendu pour ainsi dire palpable à l’enfant ; et les divers procédés, facilement et matériellement décomposé, par le maître, sous ses yeux ou par lui-même, se graveront tout naturellement dans son souvenir

La commission de 1867, elle, s’était bornée à récompenser, parmi toutes les formes plus ou moins ingénieuses, compliquées et bizarres des appareils exposés, le boulier-compteur vertico-horizontal de M. Chaumeil, inspecteur primaire à Bordeaux, lequel, par sa simplicité et sa commodité, se rapproche beaucoup de ceux que nous venons de décrire.

(Les différents bouliers par A. Lenient,  Journal des instituteurs, 25 février 1877)

- Boulier, Musée de l'école de Chartres et d'Eure-et-Loir.

- Compendium maternelle avec son boulier Pape-Carpantier.

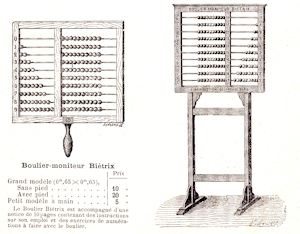
- Boulier Piétrix

Sur pied, cadre bois partagé en deux parties dans le sens de la hauteur. Dix tiges horizontales avec dix boules chacune à gauche, dix tiges avec de 1 à 10 boules à droite en ordre croissant. Les boules sont en bois naturel. Mobilier scolaire Delagrave.

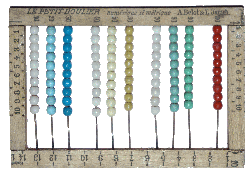
- Carte postale : Nos petits écoliers.

- Le petit boulier, numérique et métrique, A. Belot et L. Jarach,  Ferdinand Nathan.