



Mathématiques
3. Les mathématiques modernes
Enseignements


Arrêté du 2 janvier 1970
A compter de la rentrée scolaire 1970, l'enseignement des mathématiques dans les classes élémentaires sera donné conformément au programme annexé au présent arrêté.
I. - Considérations générales
L'enseignement mathématique à l'école élémentaire veut répondre désormais aux impératifs qui découlent d'une scolarité obligatoire prolongée et de l'évolution contemporaine de la pensée mathématique.
Il s'agit dès lors de faire en sorte que cet enseignement contribue efficacement au meilleur développement intellectuel de tous les enfants de six à onze ans afin qu'ils entrent dans le second degré avec les meilleures chances de succès.
L'ambition d'un tel enseignement n'est donc plus essentiellement de préparer les élèves à la vie active et professionnelle en leur faisant acquérir des techniques de résolution de problèmes catalogués et suggérés par “la vie courante”, mais bien de leur assurer une approche correcte et une compréhension réelle des notions mathématiques liées à ces techniques.
Il semble que cela soit possible si, dès le début de la scolarité, le souci majeur du maître est de donner à ses élèves une formation mathématique véritable qui leur permette, d'une manière adaptée à leur âge, à partir de l'observation et de l'analyse de situations qui leur sont familières, de dégager des concepts mathématiques, de les reconnaître et de les utiliser dans des situations variées, de s'assurer ainsi la maîtrise d'une pensée mathématique disponible et féconde.
Les connaissances mathématiques ainsi construites peu à peu se prolongent sans heurt au-delà de l'école élémentaire, mais à ce niveau déjà, les enfants pourront se rendre compte que l'univers mathématique n'est pas clos sur lui-même et mesurer le pouvoir que leur donne l'outil mathématique sur l'univers réel.
Par ailleurs, les progrès dans la connaissance du développement psychologique, de l'enfant montrent tout le bénéfice qu'il peut retirer d'un tel enseignement pour l'ensemble de sa formation.
Des expériences nombreuses, réalisées en France et à l'étranger, permettent dès maintenant l'élaboration d'un programme adapté à un enseignement rénové et accessible aux élèves. Mais la mise en œuvre d'un tel enseignement suppose que tous les maîtres aient pu y être préparés et demande, de ce fait, un certain délai. En attendant qu'une information suffisante soit donnée aux maîtres et qu'un programme entièrement rénové puisse être enseigné correctement dans nos écoles, il a paru indispensable de prendre des mesures provisoires partielles et sans doute modestes mais immédiatement applicables :alléger le programme actuel, en donner une rédaction différente qui réponde mieux aux finalités actuelles de l'école élémentaire, l'accompagner de commentaires qui, sans introduire pratiquement de terminologie nouvelle, annoncent et préparent une rénovation plus profonde et plus satisfaisante.
Dans la rédaction du programme les trois niveaux : cours préparatoire, cours élémentaire (en deux ans), cours moyen (en deux ans), sont conservés.
Pour chacun de ces niveaux les notions numériques qui constituent l'essentiel du programme sont présentées dans le paragraphe 1. Les paragraphes suivants proposent des thèmes d'activités plus divers : le paragraphe 2 concerne l'observation de l'espace et des objets géométriques, le paragraphe 3 la notion de mesure dans une perspective expérimentale. La matière de ces deux derniers paragraphes sera donc largement empruntée aux activités d'éveil. Les activités désignées jusqu'alors sous le vocable de “calcul” restent bien entendu essentielles mais, comme elles ne constituent désormais qu'une partie de l'activité mathématique des enfants, il convient de désigner la matière du programme par le terme “Mathématique”.
Il est permis d'espérer que la nouvelle rédaction du programme et l'allégement substantiel de celui-ci inviteront les maîtres à réfléchir sur le contenu mathématique de leur enseignement. Ils y seront aidés par les commentaires.
Ceux-ci ne sauraient être considérés comme un cours de mathématiques. Ils s'adressent aux maîtres et se proposent seulement de les éclairer sur l'esprit dans lequel il est actuellement souhaitable d'enseigner les mathématiques à l'école primaire. Ils ne traitent pas également de toutes les questions. Ils ont été particulièrement détaillés à propos de celles dont la présentation est à renouveler.
Pour faciliter leur étude, ces commentaires ont été rédigés non par niveau, mais par thème du programme. Ils se substituent aux instructions de 1945, actuellement en vigueur.
En dépit de son désir d'être une approche, la plus correcte et la plus précise possible, de quelques concepts fondamentaux, abstraits par nature, l'enseignement des mathématiques à l'école élémentaire demeure résolument concret.
S'il s'agit par exemple d'acquérir la notion de nombre naturel l'enfant sera appelé à manipuler effectivement et individuellement des collections d'objets distincts. Les manipulations porteront sur des collections diverses différant les unes des autres par la nature des objets, leur forme, leur couleur, leur disposition, etc. Elles seront nombreuses et variées non pour créer des automatismes mais pour que leur variété permette à l'élève, en exerçant sa réflexion sur ce qu'il fait, de reconnaître des analogies en dépit des différences, de dégager peu à peu d'une manière d'abord intuitive et confuse puis de plus en plus consciente et claire, une notion abstraite et générale, celle de nombre naturel.
C'est par des démarches de cette nature, faites d'actions et de réflexion, que l'enfant contribuera à construire son propre savoir et connaîtra la joie de découvrir et de créer.
A l'école élémentaire, l'enseignement du calcul a longtemps eu pour tâche de donner aux enfants du peuple les rudiments indispensables à leur insertion sociale. Les quatre opérations pouvaient suffire à un peuple essentiellement rural et de faible technicité, quittant pour la plupart l'école à 12 ans ou 13 ans. L'enseignement des mathématiques ne commençant véritablement qu'en sixième pour une toute petite minorité par une approche abstraite des éléments d'arithmétique et de géométrie jugés indispensables à la construction ultérieure.
Or, l'avènement accéléré de la société industrielle exige une formation généralisée d'un plus haut niveau. Cette exigence conduit à retarder l'insertion sociale pour la totalité de la population scolaire et, ce faisant, laisse le champ libre à une action plus fine qui, de pratique, devient proprement pédagogique. Dès lors il ne s'agit plus de monter des mécanismes immédiatement utilisables, mais de créer les attitudes intellectuelles nécessaires à un progrès ultérieur. Or, corrélativement, le développement de la psychologie de l'intelligence et en particulier les apports inestimables de Piaget et de son équipe ont montré les conditions génétiques de l'accession à la pensée abstraite. La réversibilité et l'organisation mentales se reconstruisent chez l'enfant dans l'activité effective de comparaison, de classement, de mise en relation, de production. Le nombre et ses propriétés ne sont plus, dans cette perspective, que les cas particuliers d'une logique plus générale qui doit se construire dans et par l'action. (Louis Legrand, Inspecteur d'académie, Le courrier de la recherche pédagogique, 1967)
Itinéraire mathématique
Collection M.-A. Touyarot, Agrégée de mathématiques, professeur d'école normale.
Editions Fernand Nathan.
Au Cycle préparatoire :
- CP livret 1, M.-A. Touyarot et Cl. Hameau, 1977.
Pour le cours élémentaire :
- Cours élémentaire 1e année, livre, M.-A. Touyarot, J. Béguin, institutrice d'Ecole annexe, 1972.
- Cours élémentaire 2e année, livre, M.-A. Touyarot, J. Germain et M. Le Roy, 1972.
Pour le cours moyen :
- Mathématique au cours moyen 2e année, M.-A. Touyarot et Cl. Hameau, 1976.
Livre du maître :
- Enseignement élémentaire, premier niveau, M.-A. Touyarot, 1970.
- Eléments de mathématique, commentaires pédagogiques pour le cours élémentaire, 1971.
- Cubes réglettes K.M.L., Touyarot.








Math et calcul (1977)
Collection Robert Eiller.
Classiques Hachette.
L'arrêté du 18 mars 1977 définit les nouveaux programmes du cycle préparatoire. Une des caractéristiques essentielles réside dans le fait qu'ils définissent une pédagogie par objectifs formulés en termes de compétence et de comportement.
- Livre CP, R. Eiller, Inspecteur départemental de l'Education, professeur d'école normale, M.T. Guyonnaud, J. Mertz, S. et R. Ravenel, 1977 et 1984.
- Livre CE1, R. Eiller, R. Brini, M. Martineu, S. et R. Ravenel, 1978.
- Livre CM2, R. Eiller, S. et R. Ravenel, avec la collaboration de Gilberte Pérot, illustration Coryphe 1986
- livre du maître, CP, R. Eiller, M.T. Guyonnaud, J. Mertz, S. et R. Ravenel, 1977 et 1985.






L'univers mathématique
Collection B. Goergler.
Edition de l'Ecole.
Nous voudrions inviter la maître à motiver l'activité purement mathématique par des manipulations réellement concrètes, rendant ainsi aux blocs logiques la place qui doit être la leur à mi-chemin entre le concret et l'abstrait.
- Livre, CE2, B. Goergler, I.D.E.N., A. Viala, Conseiller pédagogique, et R. Andrieu, Directeur d'Ecole d'application, 1984.
- Livre du maître, CP, B. Goergler, 1970.
- Livre du maître, CE1 et CE2, B. Goergler et A. Viala, 1973.



Mathématiques
Collection Thévenet, Inspecteur départemental de l'Education nationale.
Illustrations de Simone Poullenot et Pierrette Boucherol.
Editions Bordas.
Conforme à l'esprit des programmes et des instructions pédagogiques de 1985,
Conçue pour répondre aux objectifs suivants :
- Donner à l'élève les bases nécesaires à une manipulation aisée des chiffres et des opérations.
- Proposer une méthode d'approche du problème en habituant l'élève à lire attentivement un énoncé et à s'interroger avant toute chose.
- Assurer la continuité parfaite du CP au CM.
- Fichier, CP, Serge Thévenet, Anthelme Garioud, Inspecteur départemental de l'Education nationale, Nicole Pitot, Institutrice de classe d'application, 1987.
.
- Fichier, CE2, S. Thévenet, A. Garioud et N. Pitot, 1992.


Mathématique
Collection H. et J. Denise et R. Polle
Editions Delagrave.
- Livre, CM1, 145e mille, 1975.
- Livre, CM2, 1976.
- Cahier, CE2, 2e cahier, 1972.
- Math, CP, dessins de J. P. Serenne, 1983.




Collection Nicole Picard, O.C.D.L. Paris.
- Activités mathématiques I, 1969.
-A la conquête du nombre I, CP, 1970.
- A la conquête du nombre II, CE1, 1970.
Ces fascicules sont destinés à informer les maîtres et les parents qui se posent des questions au sujet d'un enseignement nouveau des mathématiques au niveau élémentaire.



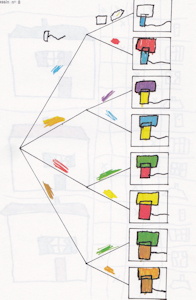
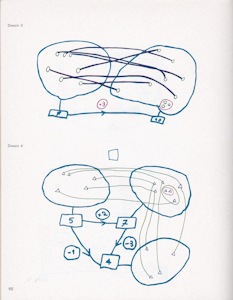







Catalogue mathématique moderne, matériel de manipulation Fernand Nathan
- Jeux mathématiques, loto des ensembles papillons, les multifamilles, ressemblances et différences, jeu de cartes logiques, poker logique, les phrases mathématiques.
- Initiation programmée aux ensembles, J. Clarke et M.-A. Touyarot, 1968.
- Matériel KML
- Les multifamilles K.M.L., 6 jeux de 24 cartes présentés en coffret.
- Ressamblances et différences, 4 jeux de 32 cartes chacun.




La mathématique
Collection Caparros
Editions Bordas.
Priorité au calcul numérique et aux techniques opératoires. Pratique du dessin géométrique.
- La mathématique au CE1 et 2, par Gérard Caparros, professeur de mathématiques, Gilbert Kosina, Directeur d'école, Jean Mariani, Inspecteur départemental de l'Education nationale, illustrations de Josiane Pont, 1976.
- La mathématique au CE2, par Gérard Caparros, Gilbert Kosina, Jean Mariani, 1981. (programmes 1978)


Programmes et instructions à l'école élémentaire
Arrêté du 15 mai 1985
Mathématiques
NATURE ET OBJECTIFS
L'enseignement des mathématiques vise à développer le raisonnement et à cultiver chez l'élève les possibilités d'abstraction. Il apporte une exigence de rigueur dans la pensée et de justesse dans l'expression. Il fait acquérir des connaissances et des compétences dans les domaines numérique et géométrique, tout en aidant l'élève à se forger des méthodes de travail. Il stimule l'imagination.
INSTRUCTIONS
Les travaux et exercices donnent lieu à une reprise ordonnée des apports essentiels, transcrite et conservée par l'élève dans son cahier. Celui-ci doit être tenu avec beaucoup de soin.
Lors de l'introduction de notions nouvelles, les élèves sont mis en situation d'apprentissage actif : ils découvrent les notions comme des réponses à des problèmes.
On peut répartir ces problèmes en trois groupes :
-ceux qui permettent la construction de nouveaux outils mathématiques (par exemple l'introduction de la soustraction, de la multiplication, des nombres décimaux);
-ceux qui invitent à utiliser des acquis, à en percevoir éventuellement les limites d'utilisation, offrant ainsi au maître les moyens de contrôler le savoir (par exemple la construction d'un objet, l'agrandissement d'une figure, le premier apprentissage de la division euclidienne) ;
-ceux qui sont liés à une véritable recherche (par exemple trouver tous les patrons d'un cube).
Résoudre des problèmes suppose la maîtrise d'un certain nombre d'outils, numériques et géométriques, et l'appropriation de méthodes. Pour cela, le maître habitue les élèves à organiser les données (ce qui suppose des outils et la capacité de les choisir) ; à associer à une question posée les connaissances utiles ; à exprimer, oralement et par écrit, leurs démarches et les résultats obtenus, en essayant de les justifier.
C'est l'occasion pour l'élève de s'approprier le langage mathématique, en restant attentif aux interférences éventuelles avec la langue courante, et d'accéder à l'organisation logique des raisonnements. C'est l'occasion pour le maître de constater réussites et échecs, en s'efforçant de comprendre ce qui les détermine.
Il importe de développer l'aptitude des élèves à prouver ce qu'ils avancent ; ainsi, selon les cas et en fonction de leur maturité, ils peuvent utiliser une argumentation de type mathématique, mettre en évidence un contre-exemple, confronter le résultat avec la réalité, prêter attention à la différence entre le calcul et la mesure, etc.
Enfin, l'utilisation de l'informatique, à propos de la résolution d'un problème numérique ou géométrique, en particulier au cours moyen, permet d'initier l'élève à la recherche d'algorithmes et de développer ses capacités logistiques.
L'éveil mathématique (1970)
Collection J. Manesse
Classique Hachette.
L'orientation actuelle de l'enseignement implique une attitude pédagogique nouvelle. Le maître devient l'animateur de la classe et l'éveil mathématique se fonde essentiellement sur la participation de l'enfant. Celui-ci crée des situations, les analyse ; il agit sur les choses, découvre, s'exprime, construit peu à peu son savoir avec l'aide du maître. A tout moment, l'activité de l'intelligence précède l'activité de la mémoire.
- Plastifiche Math 001, CP, J. Manesse, I.D.E.N. et G. Lecouvez, Conseiller pédagogique, 1972.
- Math 001, album du maître, 1970.
- Math 015, travaux pratiques, CM2, 1975.
- L'éveil mathématique au CE2, J. Manesse et R. Crépin, I.D.E.N., avec la collaboration de P. Barillier, Conseiller pédagogique, et M. Diez, Directrice d'Ecole normale,1979.





HORAIRES OBJECTIFS ET PROGRAMMES
Arrêté du 18 mars 1977
Les objectifs au cycle préparatoire précisent qu'à tous les niveaux de l'école primaire, il importe de partir de situations tirées du vécu de l'enfant, liées à ses intérêts spontanés ou provoqués, et de les exploiter collectivement et individuellement dans le cadre de la vie de la classe.
L'observation et l'analyse de ces situations multiples et variées auront pour objectifs généraux :
a) De faire apparaître les éléments et structures communs afin de dégager les notions essentielles que l'enfant doit acquérir ;
b) De représenter les modèles correspondants à l'aide de signes, de symboles ou sous forme schématique (diagrammes, tableaux...), et ainsi, à la fois de préciser ces notions et de les rendre conceptuellement utilisables ;
c) De répondre aux questions, de donner une solution aux problèmes qui peuvent se poser en mettant en œuvre les techniques acquises ce qui permet à l'enfant de confirmer ses connaissances.
Arrêté du 7 juillet 1978
Les objectifs pour le cycle élémentaire indiquent qu'au cycle élémentaire encore plus qu'au cycle préparatoire, les activités mathématiques quelles qu'elles soient doivent entre autres choses permettre aux enfants de développer des attitudes de recherche. C'est pourquoi on privilégiera les démarches pédagogiques à travers lesquelles les élèves sont toujours confrontés à des situations qu'ils doivent traiter.
Arrêté du 18 juillet 1980
Pour les objectifs du cycle moyen , comme aux cycles précédents, les activités mathématiques doivent permettre aux enfants :
- de réorganiser, d'enrichir et d'approfondir des connaissances antérieures (dans le domaine des nombres naturels, par exemple) ;
- d'acquérir de nouvelles connaissances (dans le domaine des nombres décimaux, de la division, par exemple) ;
- d'accumuler des expériences qui serviront de support à des formalisations ultérieures (dans le domaine de la géométrie, des nombres décimaux, par exemple) ;
- de développer des savoirs
- faire et des comportements (procédures de recherche, de preuve...) dans tous les domaines.
Dans le n°1 de septembre 1973 du Journal des Instituteurs et des institutrices, C. L. Hameau, Instituteur, attire les maîtres sur certaines pratiques qu'il considère comme abusives.
Il indique que les erreurs d'interprétation ou les abus n'ont pas un caractère de gravité que certains se complaisent à dénoncer. Ce sont, la plupart du temps, d'inévitables maladresses dues à l'inexpérience dans un enseignement qui s'est transformé.
Abus concernant la numération :
Dans l'esprit de beaucoup, l'écriture des nombres avait, auparavant, quelque chose d'intangible : sept, c'était 7, dix c'était 10. Qu'un même nombre puisse recevoir différentes écritures selon la base choisie, que quatre puisse s'écrire 10 (en base quatre) ou 11 (en base trois) ou 100 (en base 2), cela a pour beaucoup un caractère de nouveauté, d'étrangeté même, qui est comme la carte de visite de la réforme.
Les idées relatives à la numération sont les premières assimilées par les maîtres et les premières à se traduire en pratiques pédagogiques. Les maîtres y trouvent l'attrait du nouveau, de la découverte personnelle. Les enfants s'y intéressent. La tentative est donc grande d'hypertrophier ce chapitre et d'y consacrer des semaines, voir des mois, au détriment d'autres chapitres eux aussi très importants.
Certains maîtres font donc faire à leurs élèves de véritables exercices de virtuosité, alors que l'utilité principale de la numération en bases différentes de dix est d'éclairer la numération en base dix.
Elle permet de dissocier l'idée de nombres et ses différentes notations et montre que, pour compter, il faut faire le choix d'une base de numération et que ce choix est arbitraire.
Les calculs avec des nombres écrits en différentes bases permettent d'éclairer certaines techniques opératoires : il en est ainsi de la retenue dans l'addition, par exemple. Cela rend donc de grands services. Il semble, en revanche de peu d'utilité de faire effectuer de longs calculs de virtuosité dans d'autres bases que la base dix.
Il est donc raisonnable qu'au cours moyen de consacrer seulement les trois premières semaines de l'année à l'étude de la numération.
Concernant le vocabulaire :
Ce qui frappe qu'en on consulte les ouvrages qui parlent des mathématiques modernes, c'est l'avalanche de termes nouveaux avec lesquels il faut se familiariser. Certains en ont tiré le sentiment, surtout après avoir examiné les manuels, que l'école primaire doit enseigner maintenant ce nouveau vocabulaire.
Employer des mots comme "relation fonctionnelle", "réunion", réflexivité", transitivité", symétrie" (pour une relation), "relation d'équivalence", n'offre guère d'intérêt. Ce vocabulaire est indispensable pour le maître qui doit dominer les idées sous-jacentes aux exercices qu'il propose à ses élèves, mais il ne l'est pas pour les enfants.
Dans le même ordre d'idées, on voit trop souvent apparaître l'inflation des signes. Il ne nous semble nullement nécessaire d'embarrasser l'esprit des enfants avec des signes tels que celui d'appartenance : E ou d'inclusion C, ou avec des signes d'opération sur les ensembles, tels que l'inter section U ou la réunion.
A notre avis l'école primaire n'a pas à inculquer toutes ces connaissances formalisées. L'école primaire doit, au contraire, doter les enfants d'un grand nombre d'expériences : expérience du nombre, de l'espace, etc. Elle doit leur donner l'occasion de tâtonner, de rechercher par eux-mêmes, de découvrir l'activité mathématique et non pas de donner un savoir.
Concernant l'abandon du calcul mental :
Il s'agit d'un mal déjà ancien qui a précédé la réforme. On ne dira jamais tout le bien que les enfants peuvent retirer de la pratique constante du calcul mental.
L'exercice de calcul mental quotidien, à l'aide de l'ardoise plaît aux enfants quand il est bien mené.
Il faut souligner qu'il est indispensable d'entraîner nos élèves à la pratique du calcul. On a combattu, à juste titre, les anciennes pratiques qui consistaient à faire apprendre un mécanisme opératoire. On a montré qu'il était nécessaire de justifier les techniques opératoires. Il ne faudrait pas pour autant en conclure qu'il est superflu d'entraîner les enfants à la pratique du calcul en proposant des exercices nombreux et variés, qui puissent les amener à réfléchir sur les propriétés mises en œuvre.
Mise en place de la réforme
La réforme des mathématiques en France, commence en 1940, par des jeunes mathématiciens regroupés sous le nom de "Bourkaki" qui veulent réviser les programmes de l'enseignement supérieur.
En 1952, trois grands mathématiciens français, Jean Dieudonné, Gustave Choquet et André Lichnerowicz se réunissent à Melun avec le psychologue suisse Jean Piaget pour parler de l'enseignement des mathématiques dans les classes élémentaires.
Une commission est formée en 1967, par le ministre de l'Education nationale, Christian Fouchet, connue sous le nom de "Commission Lichnerowicz". Elle publie son premier rapport en mars 1967. Elle demeure active jusqu'en 1973.
Les événements de mai 1968, qui mettent en évidence la nécessité d'une réforme du système scolaire, accélèrent le mouvement. A la rentrée de 1969, les projets de programme de la commission Lichnerowicz sont officialisés pour la sixième et la seconde, les autres classes devant suivre année par année.
En 1970, la réforme est lancée dans l'enseignement primaire, où elle doit se faire progressivement. Pour soutenir la réforme, des "Instituts de recherche sur l'enseignement des mathématiques" (IREM), en gestation depuis 1966 sous l'impulsion de l'Association des Professeurs de Mathématiques de l'Enseignement Public (A.P.M.E.P.), sont créés officiellement en 1969. D'abord au nombre de trois (Paris, Lyon, Strasbourg), ils seront en octobre 1974, un par académie. Ils ont pour mission la formation des enseignants, la recherche et l'expérimentation pédagogique, et l'élaboration et la diffusion d'une documentation.
Cette réforme est pilotée sans grande concertation avec les enseignants, à charge pour les inspecteurs de l'Éducation nationale de transmettre les instructions et de mettre en place les stages de recyclage. Cette approche ne facilite pas son adoption par la base.
À l'école primaire, la théorie des ensembles et les bases de numération autres que la base 10 constituent l'aspect le plus visible de la réforme. Le programme commence par l'étude de la théorie naïve des ensembles en parallèle de l'arithmétique. Par exemple, la base 2, essentielle en électronique et en informatique, est présentée dès le CE1 (7 ans), ainsi qu'une rapide introduction à la base 3. Une première initiation à la théorie naïve des ensembles est enseignée au moyen de diagrammes bigarrés, également dès le CE1. On espère ainsi développer la pensée logique et les facultés d'abstraction des élèves.
Les critiques montent
Plusieurs membres de la Commission Lichnerowicz se désolidarisèrent du groupe au début des années 1970, notamment Jean Dieudonné.
Les protestations viennent de ceux qui ont toujours été opposés à la réforme; ainsi, le 6 mars 1973, devant l'Académie des sciences, J. Leray déclare : La réforme en cours met gravement en danger l'avenir économique, technique et scientifique du pays".
Mais des protestations naissent également chez des enseignants qui ne sont pas des conservateurs et qui ne s'opposent pas à une réforme de l'enseignement des mathématiques.
Plus encore, des promoteurs directs de la réforme commencent à s'émouvoir. En octobre 1972, le comité national de l'A.P.M.E.P. lance un cri d'alarme sur la façon dont la réforme se met en place.
En 1973, G. Choquet écrit, dans l'Ecole libératrice :
Je suis effaré par ce que je constate dans l'enseignement à l'école primaire et dans le premier cycle du Secondaire. Certes, j'ai été l'un des promoteurs de la réforme de l'enseignement mathématique, mais ce que je préconisais était simplement un élagage de quelques branches mortes et encombrantes, et l'introduction d'un peu d'algèbre ... Bien sûr, en soi les nouveaux programmes et les instructions correspondantes sont - malgré quelques erreurs de bonne taille - plus satisfaisants que les anciens ; mais il y a eu toute une atmosphère nocive qui a accompagné leur mise au point: en particulier une attaque contre la géométrie et contre le recours à l'intuition ; on a dit aux enseignants qu'ils étaient des minables s'ils étudiaient les triangles, que l'algèbre linéaire remplaçait toute l'ancienne géométrie... Le résultat est tel que, sans une saine réaction de la base, je pense que la génération actuelle de nos écoles recevra une formation mathématique ne la préparant, ni à la recherche mathématique, ni à l'utilisation des mathématiques dans la technique ou les sciences expérimentales.
Lichnerowicz démissionna en 1973, ce qui sonna le glas de la deuxième phase de la réforme.

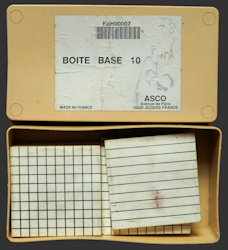

- Boîtes matériel pédagogique ASCO pour différentes bases.
"Ce n’est pas pour former des mathématiciens professionnels purs ou appliquées qu’un renouvellement de l’enseignement mathématique à l’école a été nécessaire ; ce l’est surtout et d’abord pour les futurs citoyens, [...] qui ne devront pas subir passivement les trames variées qui leur seront proposées ou imposées, qui ne devront pouvoir dire non à tels manipulateurs trop adroit d’ordinateurs, et ne pas capituler devant un terrorisme pseudo-scientifique."
André Lichnérowicz, L’école libératrice, janvier 1973
Retour à la normalité
Il a bien fallu reconnaître qu’une présentation formelle des mathématiques est totalement inadaptée. Modifications en modifications les mathématiques sont progressivement remaniées.
Autant les mathématiques modernes ont été traumatisantes, autant le retour à la raison passe inaperçu.
La réforme a fait prendre conscience, à tous les niveaux, que la cohérence mathématique ne suffit pas pour fonder un programme, qu’abstraction et concepts ne doivent pas intervenir de façon prématurée, que les élèves puissent donner du sens à leurs apprentissages.
Le dysfonctionnement mis à jour à l’occasion de la réforme des maths modernes n’est pas le manque de concertation qui a réellement existé, mais le fait que celle-ci a été accaparée par les seuls savants universitaires. Ce que l’on sait aujourd’hui est que chacun des acteurs a son mot à dire ; les savants qui expriment les besoins de la science, les didacticiens qui réfléchissent à sa faisabilité pour un public donné, le ministère qui représente la société et les enseignants qui sont les premiers impliqués, doivent travailler en concertation. Chacune de ces quatre parties est incontournable, en oublier une rend un projet inadapté ou inapplicable. (Cercle de Réflexion Universitaire du lycée Chateaubriand de Rennes - 1994-1995)
Les mathématiques modernes posent problèmes
La réforme engendre une étrange pédagogie active qui, sous prétexte de faire construire à l'enfant ses notions mathématiques, lui apprend en réalité à décrire dans un langage mathématique plus ou moins tarabiscoté des situations pseudo-concrètes souvent abracadabrantes.
De nombreux enseignants et parents d'élèves se plaignent de cette nouvelle façon d'enseigner les mathématiques. Outre la résistance naturelle au changement, le changement est trop radical. Les parents ne comprennent rien à ce que leurs enfants étudient à l'école et sont frustrés de ne pouvoir leur apporter aucun soutien. L'abstraction est à leurs yeux excessive et trop éloignée des compétences moyennes des élèves.
L'enseignement des mathématiques modernes est rapidement taxé d'élitisme car s'il convient aux élèves doués en mathématiques, il pose en revanche souvent des difficultés aux autres élèves.
Les mathématiques deviennent très logiquement un instrument privilégié de la sélection dans le système scolaire rénové de la société moderne.
A l'époque de l'instauration du collège unique, cet élitisme semble incompatible avec la massification de l'enseignement.
- L'outil mathématique, livre de l'élève, par J.-P. Leblond et J. Delarme, CM, SUDEL, 1975.

Les mathématiques modernes à l'école primaire
grace aux "nombres en couleurs" de G. Cuisenaire.
L. Vandendriessche, I.DEN, S. Vandendriessche, Conseillère pédagogique.
Lachaux et Niestlé éditeurs
La méthode découle directement de la psychologie de Piaget. Tout est fondé sur l'activité personnelle de l'enfant. Toute notion nouvelle est présentée sous forme de manipulations, de dessins, de découpages, de jeux, de calculs de découvertes, le concept émergeant alors peu à peu et pouvant ensuite être traduit dans le langage convenable et officiel.
- Livre de l'élève n°4, CM1, 1971.
- Livre du maître, 1972.


